[알고리즘]느리게 갱신되는 세그먼트 트리 lazy propagation 알고리즘

안녕하세요!👋
오늘은 lazy propagation 알고리즘에 대해 알아보도록 하겠습니다

🙏요약

이번 글에서는 일반적인 세그먼트 트리와 lazy propagation알고리즘을 적용한 세그먼트 트리를 비교하여 알아보고 예시코드를 통해 자세히 설명하도록 하겠습니다

1. lazy propagation 설명
2. 일반적인 세그먼트 트리와 비교

📔Lazy Propagation

이 글을 보기 전에 세그먼트 트리에 대해 모른다면 세그먼트 트리부터 보고 와야 합니다. 일반적인 세그먼트 트리는 구간의 합,곱,최대,최소 등을구할때 일일히 모두 비교해볼 필요 없이 O(logN)만에 구할수 있습니다. 하지만 이러한 세그먼트 트리에도 약점이 있는데 값이 수정되었을 때 이를 업데이트 하는데 시간이 매우 많이 걸린다는 것입니다. 하나의 원소를 업데이트 하면 위쪽 노드들의 값도 모두 반영해 주어야 하므로 O(logN)의 시간복잡도가 걸리게 되고 만약 여러개를 업데이트하려면 O(NlogN)의 시간복잡도가 걸리게 됩니다.
이러한 것을 해결해 줄 수 있는 알고리즘이 lazy propagation(느리게 갱신되는 세그먼트 트리) 입니다.
사용하면 좋은 경우는 구간의 값을 갱신할때 아주 유용한데 하나씩 천천히 알아보도록 하겠습니다.

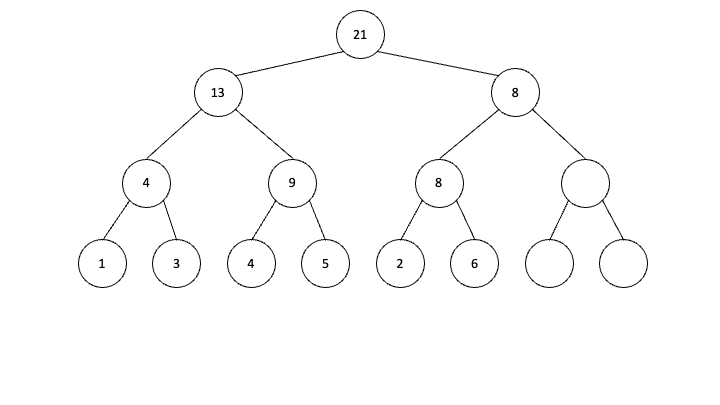
1 3 4 5 2 6 이렇게 6개의 원소가 들어있는 구간합 세그먼트 트리를 예로 들어보겠습니다. 만약 2번째부터 5번째 까지 -1을 하려고 한다면 어떻게 업데이트를 해야할까요

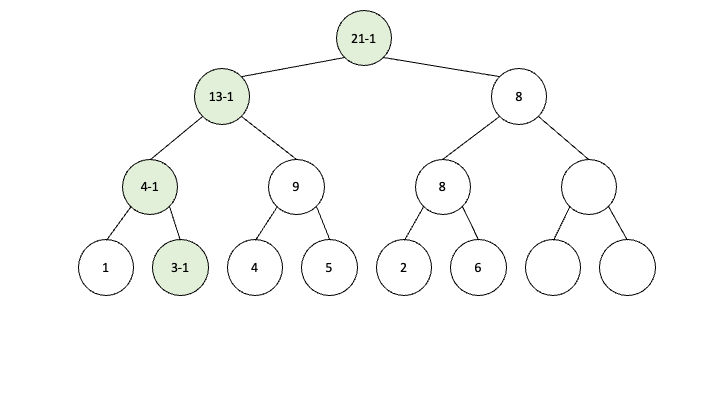
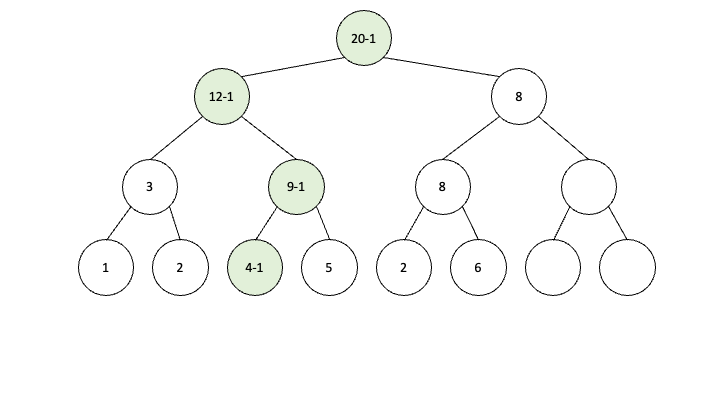
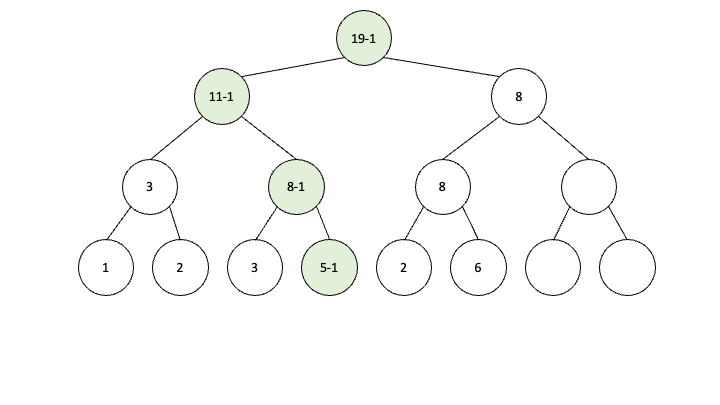
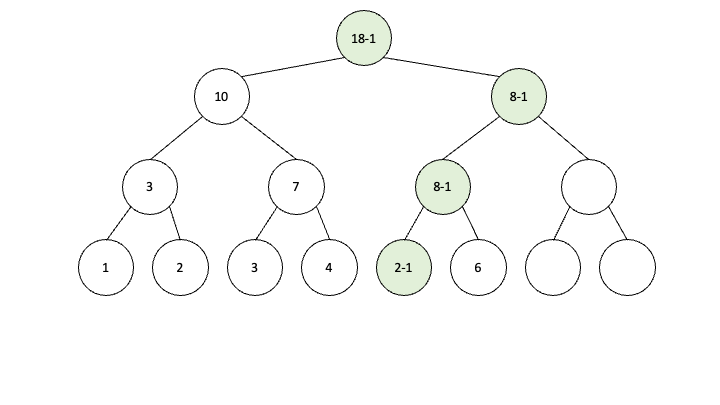
이렇게 하나하나씩 그것도 위로 올라가면서 업데이트를 해줘야 합니다. 여기서 시간이 너무 많이 걸리는 것을 lazy propagation은 획기적으로 줄여줍니다.

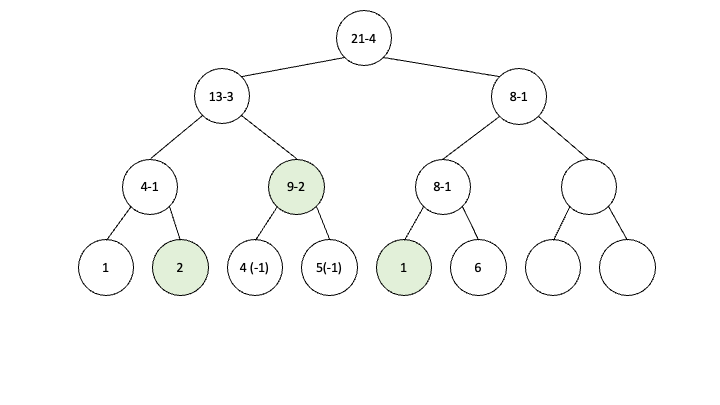
바로 이러한 방법으로 구간 안에 들어오는 노드는 (-1)x(자식구간)값을 업데이트 하고 그 자식은 -1이라는 값을 lazy에 적어만 놓고 이값은 후에 다시 노드에 접근했을 때 업데이트 해 주면서 시간복잡도를 줄이게 됩니다.
이러한 방식이면 구간을 업데이트에 O(logN)시간복잡도 만에 구간 값을 업데이트 할수있게 되는 것입니다
사진으로만 보면 조금 어려운데 코드를 보면 생각보다 간단합니다 구간 안에 들어오는 곳이면 (-1)x(가지고있는 자식들의 구간(end-start+1))값을 업데이트 해주고 그 자식들에 -1을 입력해 놓는 것입니다.
만일 업데이트 하려는 범위을 초과하는 노드라면 재귀적으로 범위를 나누어 세그먼트 트리처럼 양쪽으로 업데이트 해주고 자식이 업데이트 된 값을 통해 자신의 값을 찾으면 됩니다

🔎일반적인 세그먼트 트리와의 비교

lazy propagation은 사진이나 글로만 설명하기는 어렵습니다. 코드를 보면서 익혀보겠습니다 일반적인 세그먼트 트리의 코드와 어떻게 달라지는지 보면 금방 알 수 있을 것입니다 다음은 일반적인 세그먼트 트리의 구간합을 구하는 코드입니다

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
typedef long long ll;
class nomal_segmenttree{
private:
    vector<ll> stree;
    int size;
    int N,M;
public:
    nomal_segmenttree(){
        int a,b;
        std::cin >> N >> a >> b;
        M = a+b;
        size = 1<<(int)ceil(log2(N));
        stree.resize(size*2);
        set_val();
    }
    void set_val(){
        for(int i=0;i<N;i++)
            std::cin >> stree[size+i].val;
        for(int i=size-1;i!=0;i--)
            stree[i].val=stree[i*2].val+stree[i*2+1].val;
    }
    ll interval_sum(int node,int start,int end,int left,int right){
        if(right<start || end<left)
            return 0;
        if(left<=start && end<=right)
            return stree[node].val;
        int mid=(start+end)/2;
        return interval_sum(node*2,start,mid,left,right)+interval_sum(node*2+1,mid+1,end,left,right);
    }
    void update(int node,int start,int end,int left,int right,ll diff){
        if(right<start || end<left)
            return ;
        if(start==end){
            stree[node].val+=diff;
            return ;
        }
        int mid = (start+end)/2;
        update(node*2,start,mid,left,right,diff);
        update(node*2+1,mid+1,end,left,right,diff);
        stree[node].val=stree[node*2].val+stree[node*2+1].val;
    }
    void start_query(){
        int a,b,c;
        ll d;
        for(int i=0;i<M;i++){
            std::cin >>a;
            if(a==1){
                std::cin >> b >> c >> d;
                update(1,1,size,b,c,d);
            }
            else{
                std::cin >> b >> c;
                std::cout << interval_sum(1,1,size,b,c)<<'\n';
            }
        }
    }

};

보통은 업데이트 시 while(index>1)로 아래에서 부터 업데이트 하는 경우가 많지만 lazy propagation과의 비교를 위해 위에서부터 업데이트해 내려가는 형식으로 작성하였습니다.
구간을 재귀 방식으로 내려가면서 마지막에 업데이트해야할 지점(start==end)에 도착했을 때 값을 변경해주고 위로 올라가며 재귀가 끝나면서 자기자신이 업데이트 되는 구조입니다.
일반적으로 세그먼트 트리 문제를 한두문제만 접해봣으면 금방 알 수 있는 구조일 것입니다.

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
typedef long long ll;
struct _node{
    ll val=0,lazy=0;
};
class lazy_propagation{
private:
    vector<_node> stree;
    int size;
    int N,M;
public:
    lazy_propagation(){
        int a,b;
        std::cin >> N >> a >> b;
        M = a+b;
        size = 1<<(int)ceil(log2(N));
        stree.resize(size*2);
        set_val();
    }
    void set_val(){
        for(int i=0;i<N;i++)
            std::cin >> stree[size+i].val;
        for(int i=size-1;i!=0;i--)
            stree[i].val=stree[i*2].val+stree[i*2+1].val;
    }
    ll interval_sum(int node,int start,int end,int left,int right){
        propagation(node,start,end);
        if(right<start || end<left)
            return 0;
        if(left<=start && end<=right)
            return stree[node].val;
        int mid=(start+end)/2;
        return interval_sum(node*2,start,mid,left,right)+interval_sum(node*2+1,mid+1,end,left,right);
    }
    void update(int node,int start,int end,int left,int right,ll diff){
        propagation(node,start,end);
        if(right<start || end<left)
            return ;
        if(left<=start && end<=right){
            stree[node].val+=(end-start+1)*diff;
            if(start!=end){
                stree[node*2].lazy+=diff;
                stree[node*2+1].lazy+=diff;
            }
            return ;
        }
        int mid = (start+end)/2;
        update(node*2,start,mid,left,right,diff);
        update(node*2+1,mid+1,end,left,right,diff);
        stree[node].val=stree[node*2].val+stree[node*2+1].val;
    }
    void propagation(int node,int start,int end){
        if(stree[node].lazy){
            stree[node].val+=(end-start+1)*stree[node].lazy;
            if(start!=end){
                stree[node*2].lazy+=stree[node].lazy;
                stree[node*2+1].lazy+=stree[node].lazy;
            }
            stree[node].lazy=0;
        }
    }
    void start_query(){
        int a,b,c;
        ll d;
        for(int i=0;i<M;i++){
            std::cin >>a;
            if(a==1){
                std::cin >> b >> c >> d;
                update(1,1,size,b,c,d);
            }
            else{
                std::cin >> b >> c;
                std::cout << interval_sum(1,1,size,b,c)<<'\n';
            }
        }
    }

};

다음은 lazy propagation을 적용한 코드입니다 무엇이 달라졌는지 확인해 보기 바랍니다. propagation이라는 함수가 추가되었고 이는 lazy가 있는 부분이면 lazy를 0으로 만들고 자기 자신에 업데이트 하면서 lazy값을 자식들이 있는경우 아래 자식들에게 주는 형식입니다. 이런 방식이라면 리프 노드까지 가지 않고도 원하는 부분에서 원하는 곳까지만 업데이트 한다음 결과를 찾을 수 있습니다.

또한 interval_sum을 구할 때에도 propagation을 하면서 혹시라도 아직 업데이트가 되지 않은 곳을 마주치면 업데이트 하고 값을 구하도록 하는 것입니다.
난이도가 있는 세그먼트 트리에서 알고리즘을 적용한 부분이므로 쉽게 이해하기는 어려운 부분이지만 세그먼트 트리 문제에 정말 많이 나오는 유형이므로 알아두면 좋겠습니다
그럼 다음에 더 좋은 글로 찾아오도록 하겠습니다!👊

긴글 봐주셔서 항상 감사합니다 앞으로도 유용한 내용을 많이 공유하겠습니다 그럼 안녕 👋