[알고리즘] LCA 알고리즘 정리
업데이트:
안녕하세요!👋
백준을 복습하면서 잊어버렸던 알고리즘들을 정리해보려고 합니다 트리구조에서 DP까지 활용되는 문제인 LCA알고리즘에 대해 알아보겠습니다
🙏요약
이번 글에서는 LCA알고리즘의 동작원리 대해 알아보고 예시코드를 통해 자세히 설명하도록 하겠습니다
- LCA알고리즘의 원리
- 예시코드를 통한 설명
📔LCA 알고리즘
LCA(Lowest Common Ancestor) 알고리즘은 우리말로 최소 공통 조상 입니다 트리구조의 그래프를 떠올리면 되구요
대부분 여기서 느낌이 오실껀데요 트리의 두 노드에서 올라가며 가장 빨리 만나는 조상을 찾는 문제입니다
그냥 트리의 각 노드에 parent노드를 저장해놓고 하나씩 올라가며 탐색하면 될 것 같지만 훨신 빠른 O(logN)의 시간복잡도로 구하는 방법이 존재하여 lca알고리즘이라는 이름으로 불립니다
같이 알아봅시다👊
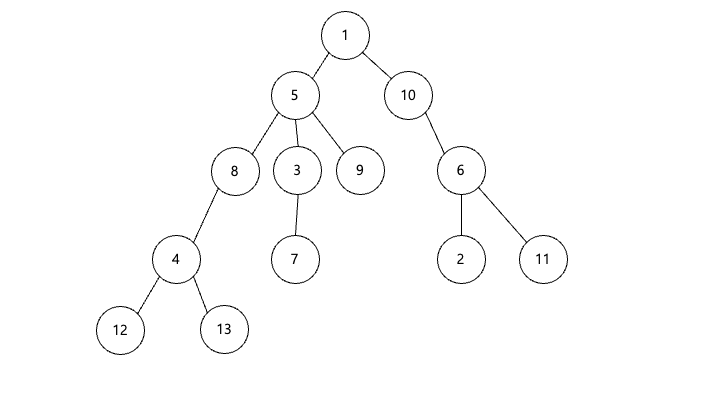
위와같은 트리가 존재한다고 했을 때 우리가 알아야 할 정보가 있습니다
먼저 위 사진과 같이 노드들을 연결 시켜준 후
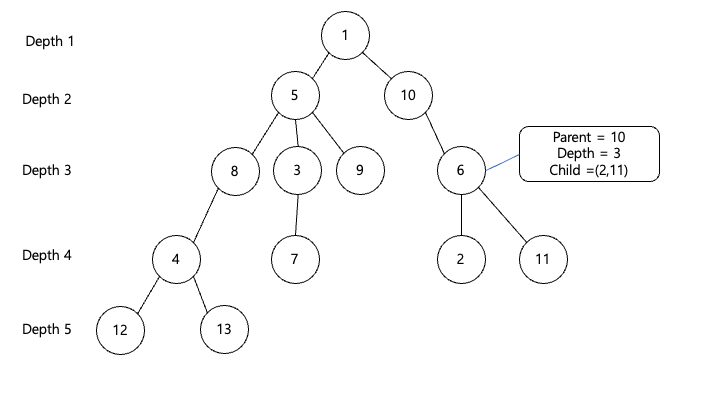
트리의 노드마다 부모노드와 자식노드 그리고 자신의 깊이를 저장해 놓아야 합니다 이러한 작업을 노드를 다 연결시킨 후 진행하게 됩니다
✨왜냐하면! 직접 구현해보면 알겠지만 연결된 노드를 받으면서 위와같은 정보를 저장할 수가 없습니다
차례대로 위에서부터 연결된 정보를 주지 않기 때문에 밑에서부터 연결시키고 위가 연결되고 하는 상황이 나올 수 있어 일단 연결 정보를 모두 받은 후 maketree라는 함수를 통해 위와같은 정보를 업데이트하여 담아두게됩니다
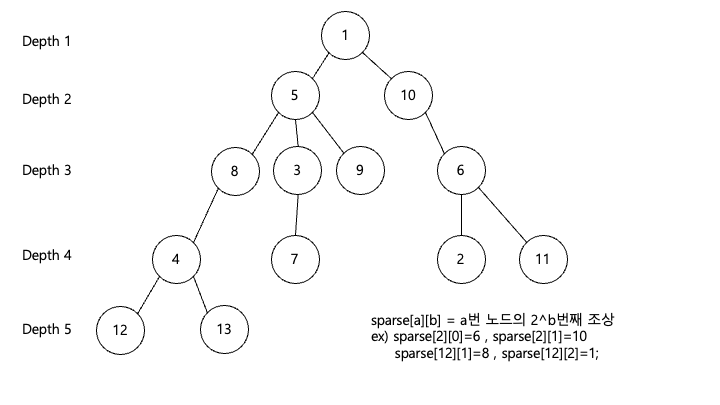
이후에는 sparse라는 2차원 배열을 만듭니다 한국말로 sparse는 희미한? 희박한? 이라는 뜻을 가집니다 왜 이런 이름으로 배열이 지어졌는지는 모르겠으나 lca알고리즘에서 통용적으로 sparse라는 이름으로 조상 노드를 저장하는 2차원 배열을 부릅니다
이 sparse배열이 정말 획기적으로 조상을 찾는 시간을 줄여주는 역할을 하는데요
각 노드의 조상중 2의 제곱배수로 조상의 위치를 저장해 두어 아무리 위에있는 조상이라도 금방 찾아갈 수 있도록 합니다
어떤 노드의 7번째 위에 조상을 찾고싶으면 보통 7번을 올라가서 찾게 되는데요 이 sparse배열을 이용하면 4번 >2번 > 1번 위로 바로 올라가서 3번만에 찾아내게 됩니다
이를 dp방식으로 sparse배열에 저장해두며 구현을 하게 되는데요 처음엔 가장 헷갈리는 부분이 되겠습니다
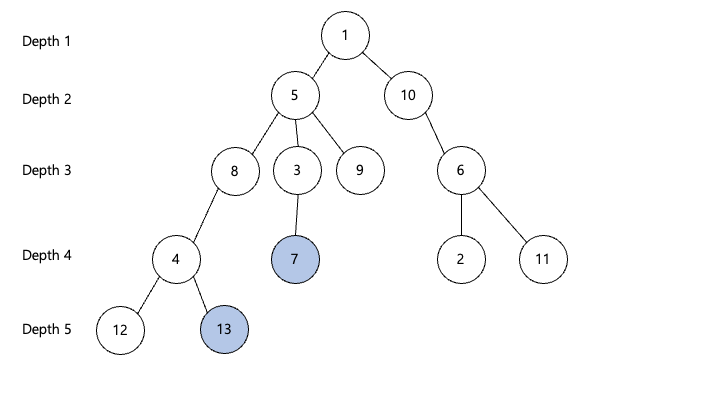
위의 sparse배열까지 이해가 되었다면 실제로 찾아보도록 하겠습니다
13과 7노드의 lca를 찾아보면
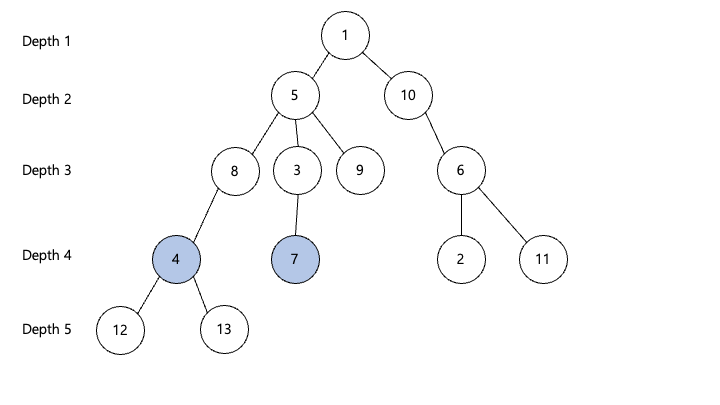
먼저 depth가 더 깊은 노드를 같은 depth가 되도록 조상을 찾아 올라옵니다 (이때도 sparse배열을 사용하여 logN만에 찾아서 올라옵니다)
그 후 두 노드가 같은지 비교하고 만약 다르다면 이제 점차 위로 찾아 올라갑니다
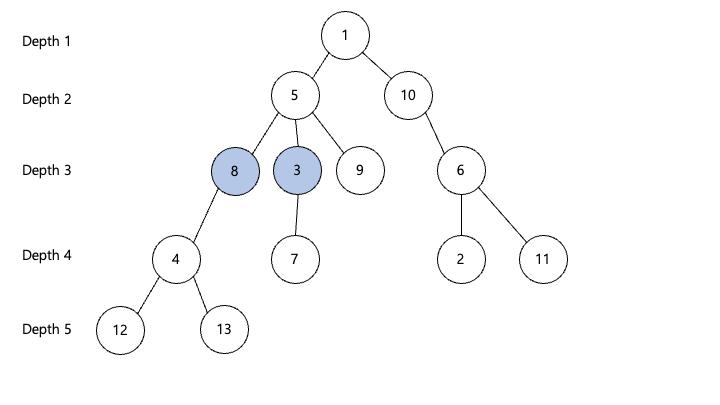
sparse배열을 이용하여 가장 위에서부터 아래로 !!같지 않는!! 조상이 나올때까지 찾아냅니다 (예시에서 1조상위라 헷갈릴 수도 있는데 sparse배열의 가장 높은곳 부터 찾아내려오는 형식입니다)
당연히 가장 높은 곳은 1로 서로 같으니까 그 밑에 5.. 등으로 같지 않는 조상중에 가장 위쪽을 찾습니다 코드를 이해하는게 좀더 편한데요!
8번째 위 ..4번째 위 .. 2번째 위 .. 1번째 위 .. 순서대로 같지 않는 조상일 경우 업데이트를 해주며 올라가다보면 결국 같지않는 가장 높은 조상이 나오게 됩니다
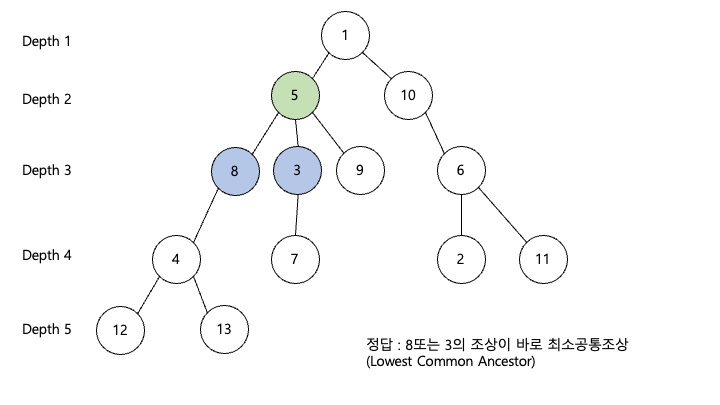
이제 이렇게 같지 않는 조상중 가장 위 조상을 찾아내었다면 이제 둘중 하나 위의 조상이 lca로 정답이 되게 됩니다
✨코드를 통해 알아봅시다
이제 lca기본 문제의 코드를 통해 더 자세히 설명해보겠습니다
문제 : 백준 11437번
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
struct _node{
int parent;
int depth;
vector<int> edge;
};
class LCA_2{
private:
vector<_node> tree;
vector<vector<int>> sparse;
int N,MAX_pow;
int root;
public:
LCA_2(){
std::cin >> N;
tree.resize(N+1,{0,0,});
set_connect();
root=1;
MAX_pow=0;
maketree(root,0,1);
MAX_pow=(int)floor(log2(MAX_pow));
sparse.resize(N+1,vector<int>(MAX_pow+1,-1));
}
void set_connect(){
int a,b;
for(int i=0;i<N-1;i++){
std::cin >> a >> b;
tree[a].edge.push_back(b);
tree[b].edge.push_back(a);
}
}
void maketree(int cur,int parent,int depth){
tree[cur].parent=parent;
tree[cur].depth=depth;
if(depth>MAX_pow)
MAX_pow=depth;
int tmp,erase_num=-1;
for(int i=0;i<tree[cur].edge.size();i++){
tmp=tree[cur].edge[i];
if(tmp==parent){
erase_num =i;
continue;
}
maketree(tmp,cur,depth+1);
}
if(erase_num!=-1)
tree[cur].edge.erase(tree[cur].edge.begin()+erase_num);
}
int DP(int n,int pow){
if(pow==0)
return tree[n].parent;
if(sparse[n][pow]!=-1)
return sparse[n][pow];
sparse[n][pow]=DP(DP(n,pow-1),pow-1);
return sparse[n][pow];
}
int LCA(int a,int b){
if(tree[a].depth>tree[b].depth)
swap(a,b);
int tmp1,tmp2;
for(int i=MAX_pow;i>=0;i--){
tmp1=DP(b,i);
if(tree[a].depth-tree[tmp1].depth<=0)
b=tmp1;
if(tree[a].depth==tree[b].depth)
break;
}
if(a==b)
return a;
for(int i=MAX_pow;i>=0;i--){
tmp1=DP(a,i);
tmp2=DP(b,i);
if(tmp1!=tmp2){
a=tmp1;
b=tmp2;
}
}
return tree[a].parent;
}
};
int main(){
LCA_2 lca;
int n,a,b;
std::cin >> n;
for(int i=0;i<n;i++){
std::cin >>a >> b;
std::cout <<lca.LCA(a,b)<<'\n';
}
return 0;
}
struct _node{
int parent;
int depth;
vector<int> edge;
};
class LCA_2{
private:
vector<_node> tree;
vector<vector<int>> sparse;
int N,MAX_pow;
int root;
위 코드는 lca에서 사용될 변수이다
LCA 알고리즘에서 가장 기준이되는 변수는 depth이다 각 노드마다 depth를 어떻게 알 것인가가 중요한데
따라서 문제중 depth가 변하는 문제는 lca문제가 아니거나 더 좋은 방식의 풀이가 존재할 수 있다
lca에서 위와같은 node를 통해 tree를 구성하고 sparse라는 2차원 배열을 선언한다
sparse 는 dp형식의 배열인데 [a][b] 가 a번 node의 2^b번째 부모를 담는 배열이다 dp방식으로 업데이트 하며 사용할 것이다
다음으로는 문제에서 주어지는 node의 개수인 N과 입력을 모두 받고 업데이트 할 가장 깊은 깊이 max_pow, 그리고 root를 담을 배열을 선언한다
LCA_2(){
std::cin >> N;
tree.resize(N+1,{0,0,});
set_connect();
root=1;
MAX_pow=0;
maketree(root,0,1);
MAX_pow=(int)floor(log2(MAX_pow));
sparse.resize(N+1,vector<int>(MAX_pow+1,-1));
}
void set_connect(){
int a,b;
for(int i=0;i<N-1;i++){
std::cin >> a >> b;
tree[a].edge.push_back(b);
tree[b].edge.push_back(a);
}
}
다음으로는 값을 입력받는 부분이다 a b를 입력받아 양방향 연결을 해준다
void maketree(int cur,int parent,int depth){
tree[cur].parent=parent;
tree[cur].depth=depth;
if(depth>MAX_pow)
MAX_pow=depth;
int tmp,erase_num=-1;
for(int i=0;i<tree[cur].edge.size();i++){
tmp=tree[cur].edge[i];
if(tmp==parent){
erase_num =i;
continue;
}
maketree(tmp,cur,depth+1);
}
if(erase_num!=-1)
tree[cur].edge.erase(tree[cur].edge.begin()+erase_num);
}
다음으로는 트리를 만들어준다 dfs방식으로 들어가면서 처음 루트를 잡고 내려가면서 parent를 확인하고 parent를 제외한 다른 연결된 노드들을 maketree함수로 재귀로 불러주면 된다
이후에 parent노드는 연결된 노드에서 제거하고 따로 parent 변수를 만들어 넣어둔다
maketree를 하면서 계속해서 max_pow를 업데이트 하는데 가장 깊은 depth를 집어넣고 이를 log2 하여 2의 몇제곱이 최대인지 알아내는 것이다
int DP(int n,int pow){
if(pow==0)
return tree[n].parent;
if(sparse[n][pow]!=-1)
return sparse[n][pow];
sparse[n][pow]=DP(DP(n,pow-1),pow-1);
return sparse[n][pow];
}
int LCA(int a,int b){
if(tree[a].depth>tree[b].depth)
swap(a,b);
int tmp1,tmp2;
for(int i=MAX_pow;i>=0;i--){
tmp1=DP(b,i);
if(tree[a].depth-tree[tmp1].depth<=0)
b=tmp1;
if(tree[a].depth==tree[b].depth)
break;
}
if(a==b)
return a;
for(int i=MAX_pow;i>=0;i--){
tmp1=DP(a,i);
tmp2=DP(b,i);
if(tmp1!=tmp2){
a=tmp1;
b=tmp2;
}
}
return tree[a].parent;
}
이제 메인이다 dp를 활용하여 sparse 배열을 저장하며 2의 pow제곱번째 부모를 알아내고 이를 토대로 LCA를 구한다.
a와 b의 lca를 구할 때 둘 사이의 depth를 비교하여 항상 한쪽이 depth가 깊도록 바꿔준다 나는 항상 b가 depth가 더 깊도록 swap을 하였다
이후 같은 depth가 될때까지 더 깊은 depth인 b를 올려준다 pow를 줄이며 제곱씩 뛰어 올라가면 딱 같은 depth가 금방 나오게 된다
이 부분에서 하나하나씩 올라가는 것보다 pow제곱만큼 뛰어 올라가는 것이 훨신 빠르기 때문에 시간복잡도가 확 줄어드는 것이다
생각해보면 pow가 0일때 2의 0제곱은 1이므로 항상 같은 depth만큼 올라가는 것이 가능하다 헷갈리는 부분이지만 이부분이 이해된다면 lca알고리즘은 모두 이해했다고 할 수 있다
같은 depth일때 a와 b가 같은지 비교하고 다르다면 역시나 pow제곱만큼 올라가며 다를 경우 업데이트를 해주는 방식으로 올라가면 결국 마지막에는 a,b둘의 lca의 딱 1칸 아래에 도달하게 된다
이후 a,b중 하나의 parent를 return해주면 lca를 구할 수 있게 된다
여기까지가 lca이고 다양한 문제를 풀면서 익히면 금방 익숙해질 수 있다!👊
댓글남기기